9. The short answer is that the Poisson approximation is faster and easier to compute and reason about, and among other things tells you approximately how big the exact answer is. Here's a simple example: suppose you're trying to get something to happen in a video game that is rare; maybe it happens 1% of the time you do something.. The approximation theorems. Let Xi indicate success on the ith trial, so that P(Xi = 1) -pi and P(Xi = 0) = 1 - pi. Our proofs will be based. on the device of introducing random variables Yi that have the Poisson dis-. tribution with E( Yi) = pi, and are such that P(Xi = Yi) is as large as pos-. sible.

PPT Lecture Slides PowerPoint Presentation, free download ID6600397

Proof Binomial to Poisson Distribution easy understanding 64

PPT Probability and Probability Distributions PowerPoint Presentation ID5681061

Solved Exercise 6.10 (Poisson approximation of Binomial RV).

PPT Binomial Distribution Vs. Poisson Distribution PowerPoint Presentation ID1266587

Lecture 4 Poisson Approximation to Binomial Distribution

Poisson approximation to the Binomial Distribution ExamSolutions YouTube

PPT Probability Boot camp PowerPoint Presentation, free download ID859784
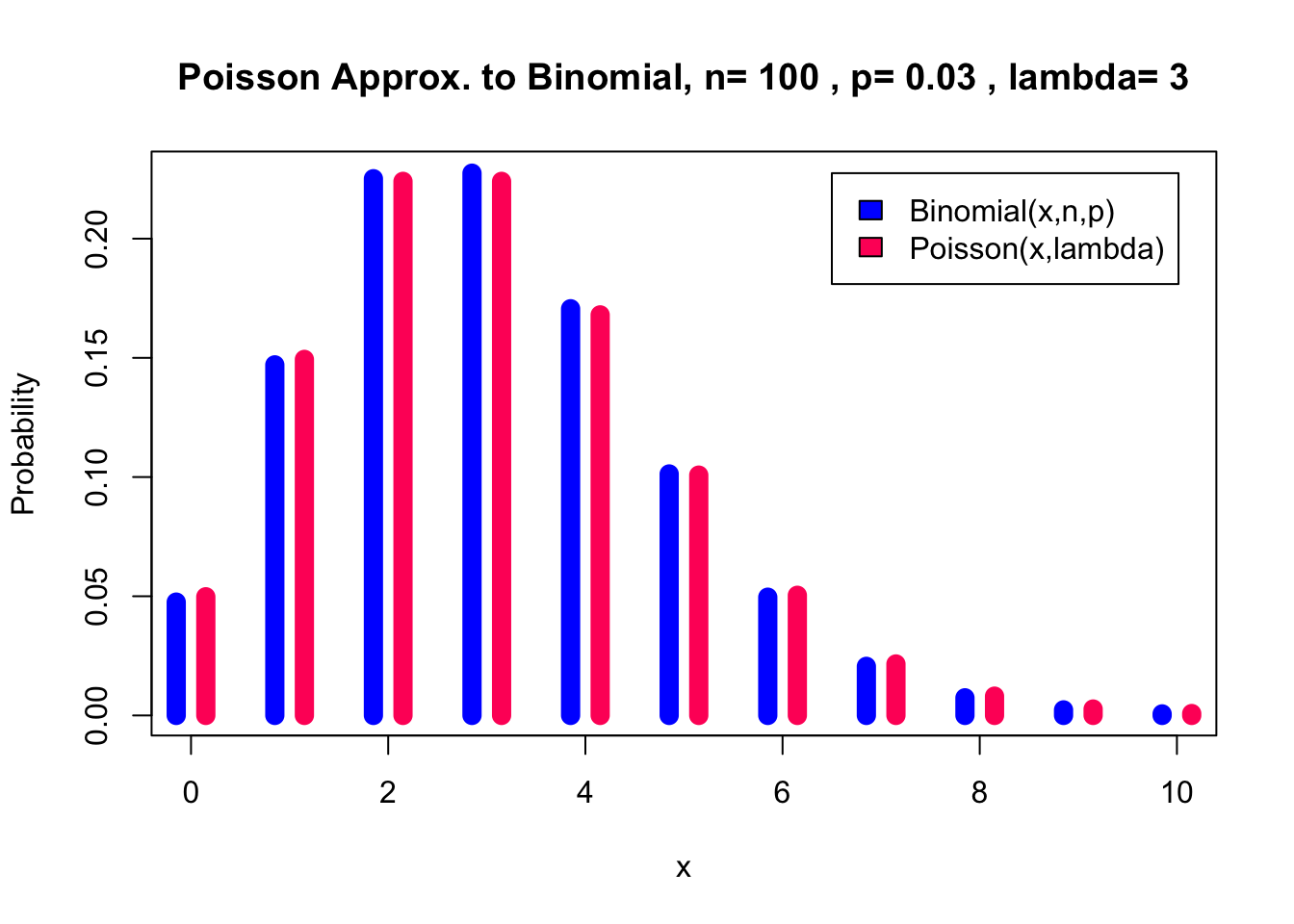
Approximating Binomial with Poisson

PROBLEM 1 BINOMIAL DISTRIBUTION VERSUS POISSON

PPT Poisson approximation to a Binomial distribution PowerPoint Presentation ID517060

Statistics Binomial & Poisson Distributions YouTube
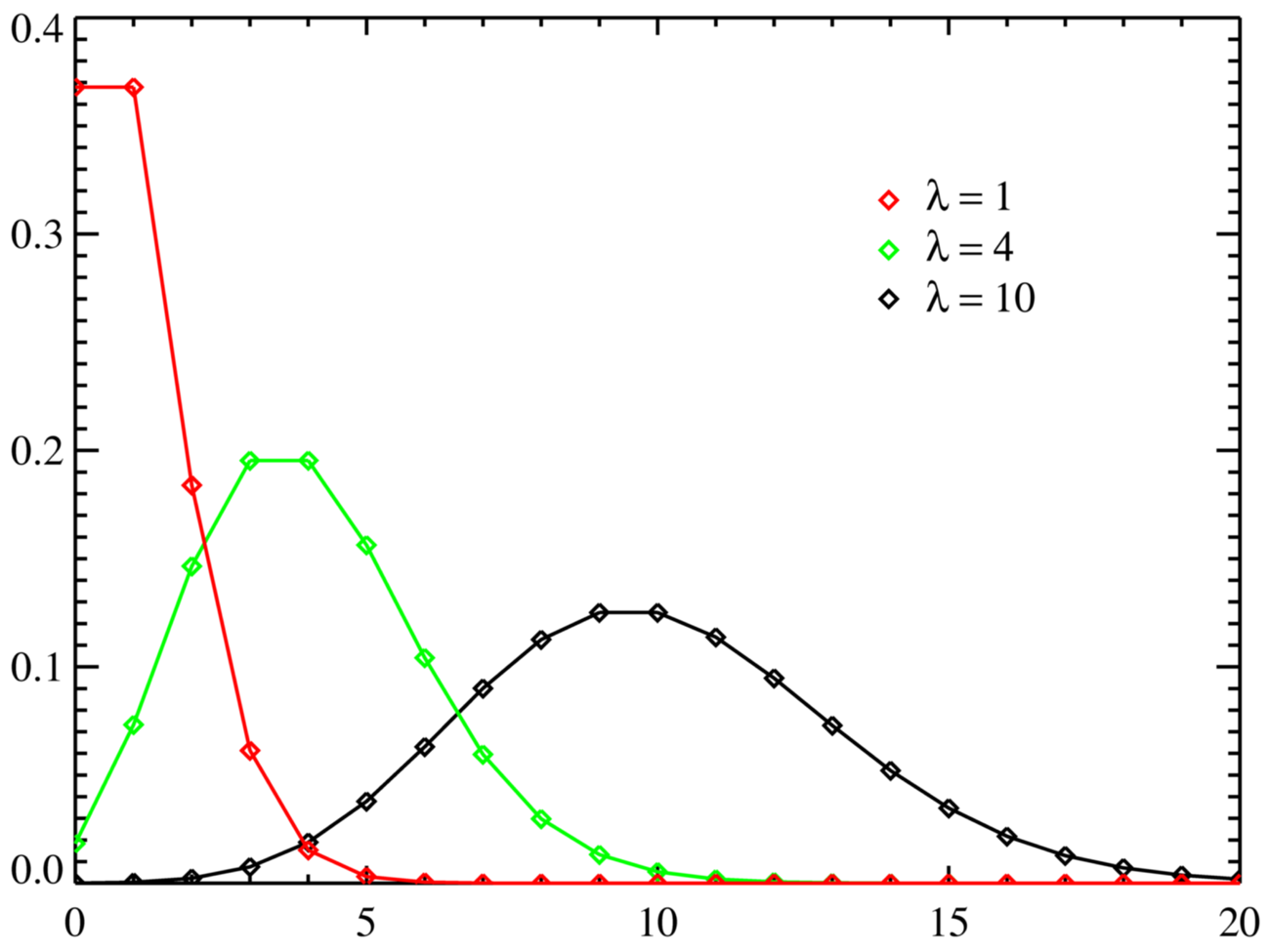
Poisson Distribution / Poisson Curve Simple Definition Statistics How To

PPT Poisson approximation to a Binomial distribution PowerPoint Presentation ID517060

Binomial and Poisson Distribution with Python by Mikdat Yücel Medium

PPT The Poisson distribution as an approximation of the Binomial. PowerPoint Presentation ID

probability How to prove Poisson Distribution is the approximation of Binomial Distribution

L21.10 The Poisson Approximation to the Binomial YouTube

STAT109 3 Random variables (4/5) Binomial + Poisson YouTube

PPT Binomial Distribution Vs. Poisson Distribution PowerPoint Presentation ID1266587
Based on the connection between the Binomial and Poisson distributions it intuitively makes sense that we should also be able to approximate the Poisson with a Normal distribution. For approximation to the binomial we need np 10 and nq 10. What is a reasonable requirement for ? Statistics 104 (Colin Rundel) Lecture 7 February 6, 2012 11 / 26. Poisson approximations 9.1Overview The Bin(n;p) can be thought of as the distribution of a sum of independent indicator random variables X 1 + + X n, with fX i= 1gdenoting a head on the ith toss of a coin that lands heads with probability p. Each X i has a Ber(p) distribution. The normal approximation to the Binomial works